二进制乘法运算

二进制乘法运算

一、定点数一位乘法

1.定点原码一位乘法

➢ 乘积的符号为相乘两数符号的异或值，数值则为两数绝对值之积
➢人工计算特点
◆ 乘积位数是乘数的二倍
◆ 相加数逐次向左偏移一位
◆ 前一部分积的最低位不再参与运算
在这里插入图片描述
机器计算需要解决哪些问题？
◆ 如何解决多个数据同时相加？
◆ 如何保存2N位乘积结果？

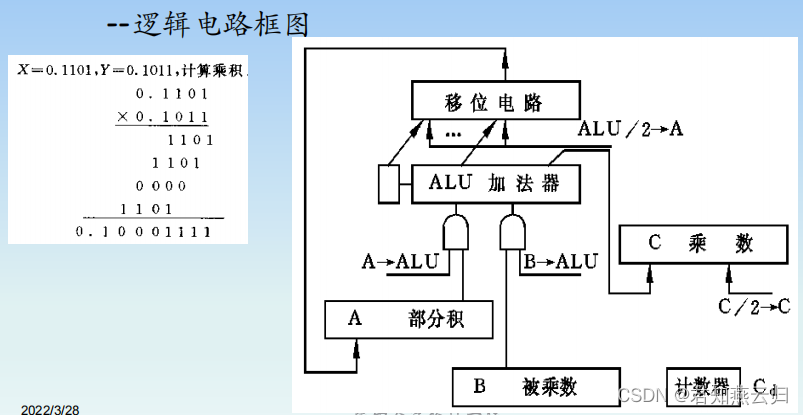
解决方法(1) ◆ 设置寄存器
➢ A寄存器：部分积
➢ B寄存器：被乘数
➢ C寄存器：乘数
解决方法(2) ◆ 每求得一个相加数，就与上次部分积相加
◆ 利用N位加法器实现两个N位数相乘。
➢ 在求本次部分积时，前一次部分积的最低位不再参与运算，因此可将其右移一位。
➢ 乘数最低位用完也没有用处了。乘数寄存器同时右移一位。
◆ A寄存器中保存乘积的高位部分，C寄存器中保存乘积的低位部分。

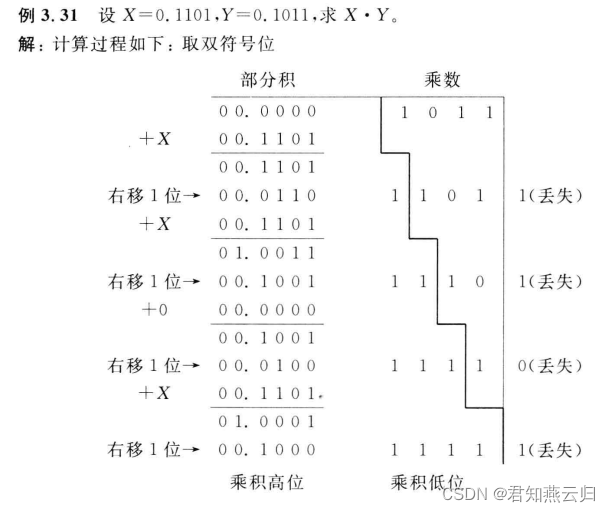
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

得出结果：
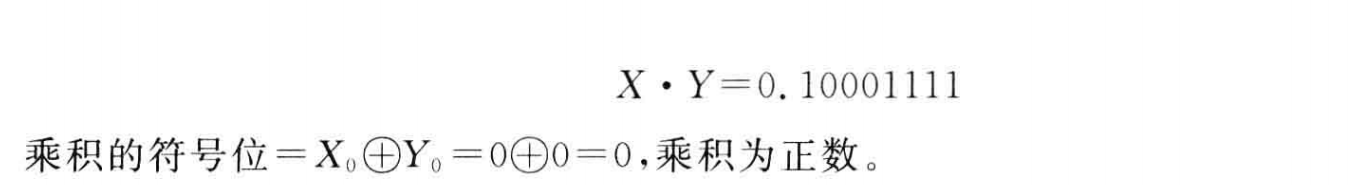
在这里插入图片描述
原码乘法是先取操作数绝对值相乘，符号位单独处理。

2.定点补码一位乘

在这里插入图片描述

定点补码一位乘法的规则
设被乘数 [X]补 = X0. X1X2… Xn
◆ 乘数 [Y]补 = Y0. Y1Y2… Yn
◆ 则 [X . Y]补 = [X]补(0. Y1Y2… Yn) - [X]补. Y0

例1： [X . Y]补 = [X]补(0. Y1Y2… Yn) - [X]补. Y0（其中Y0=0）
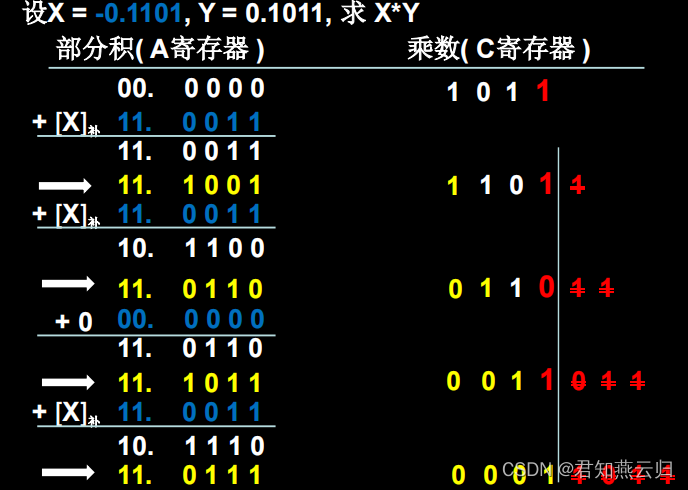
在这里插入图片描述
答案为：[X . Y]补 = 1.01110001 X . Y = -0.10001111
例2： [X . Y]补 = [X]补(0. Y1Y2… Yn) - [X]补. Y0（其中Y0=1）
在这里插入图片描述
答案为：[X . Y]补 = 0.10001111
例3：
在这里插入图片描述
根据补码一位乘公式 [X . Y]补 = [X]补(0. Y1Y2… Yn) - [X]补. Y0可知，当Y0=0时，需要进行n次加法运算；Y0=1时，需要进行n+1次加法运算。故最多需要n+1次。（n以乘数y的位数为准）

3.布斯公式

在这里插入图片描述
需要在乘数最后一位增加一位“0”，Y0也参加运算。
在这里插入图片描述

二、定点数二位乘法

1.原码两位乘法

左移一位相当于乘2，右移一位相当于除2。（此处需要结合例题反复理解）
在这里插入图片描述
在这里插入图片描述
例：
在这里插入图片描述
如果最后一次操作欠下+4X，则最后一次右移两位后还需补充+X操作，+X后不再移位。

2.补码两位乘法

根据前述的布斯算法，将两步合并成一步，可推导出补码两位乘的公式。
需要在乘数最后一位增加一位“0”，Y0也参加运算。

符号位参与运算，部分积与被乘数采用三符号位；乘数Y数值的位数为偶数设两个符号位；为奇数设一个符号位。
根据Yn-1 , Yn ,Yn+1判断
Yn-1 Yn Yn+1 组合
0 0 0 0 部分积+0，右移两位
0 0 1 1 部分积+[X]补，右移两位
0 1 0 1 部分积+[X]补，右移两位
0 1 1 2 部分积+2[X]补，右移两位
1 0 0 -2 部分积+2[-X]补，右移两位
1 0 1 -1 部分积+[-X]补，右移两位
1 1 0 -1 部分积+[-X]补，右移两位
1 1 1 0 部分积+0，右移两位
详情参考文章：补码两位乘法

例（同上布斯公式例3.34）用补码两位乘法处理
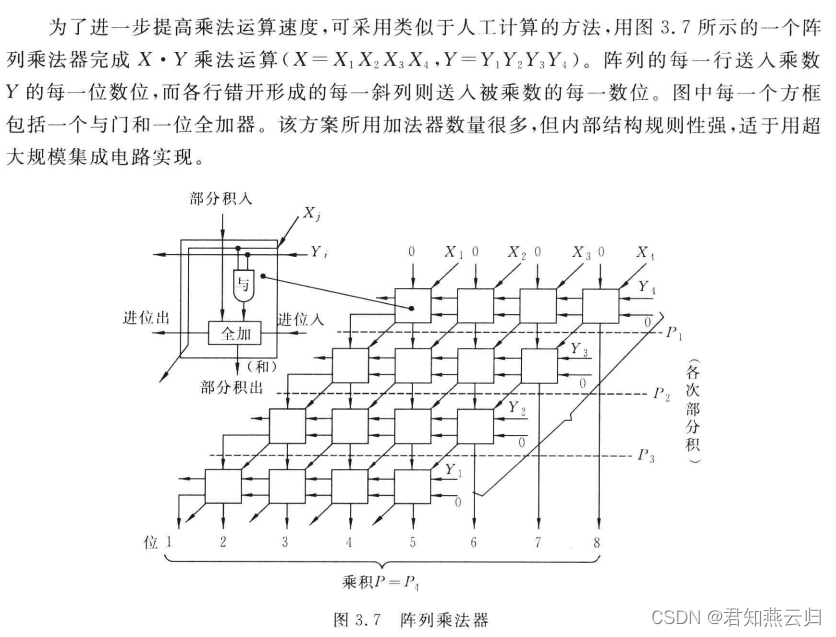
在这里插入图片描述

三、阵列乘法器

在这里插入图片描述
了解详情可参考文章：阵列乘法器