数据结构之哈夫曼树(C语言)
一、哈夫曼树的概念
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
该代码的核心在于弄懂如何构建哈夫曼树和生成哈夫曼树编码。主要通过找出两个最小值开始作为最底端叶节点,由下到上构建出哈夫曼树。
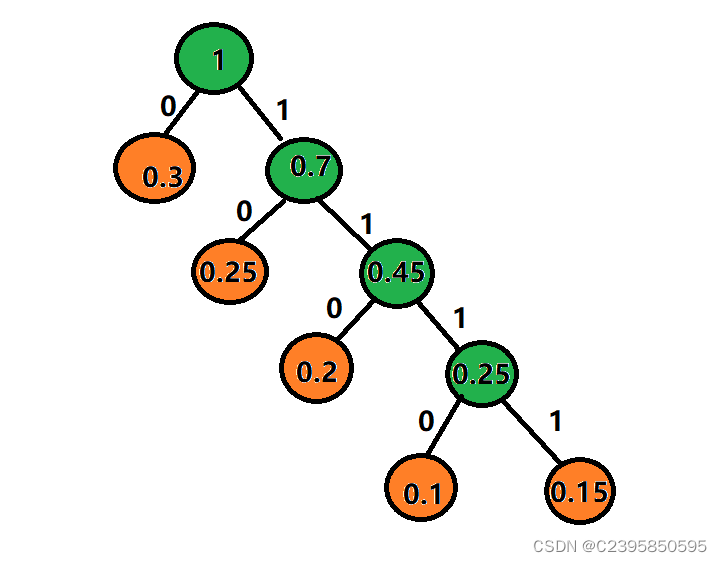
二、代码步骤
三、代码功能
1、定义二叉树和字符指针数组
typedef struct HTNode
{
double weight;
int parent;
int lc, rc;
}*HuffmanTree;
typedef char **HuffmanCode;2、二叉树的初始化
HuffmanTree initHuffmanTree(HuffmanTree& HT,int n)
{
int i;
int m = 2 * n - 1;
HT = (HuffmanTree)malloc(sizeof(HTNode)*(m + 1));
for(i = 0; i <= m; i++)
{
HT[i].lc = 0;
HT[i].parent = 0;
HT[i].rc = 0;
HT[i].weight = 0;
}
return HT;
}3、查找最小两个值的下标(min1<min2)
void Select(HuffmanTree& HT, int n, int& min1, int& min2)
{
int min;
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0)
{
min = i;
break;
}
}
for (int i = min + 1; i <= n; i++)
{
if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)
min = i;
}
min1 = min;
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0 && i != min1)
{
min = i;
break;
}
}
for (int i = min + 1; i <= n; i++)
{
if (HT[i].parent == 0 && HT[i].weight < HT[min].weight&&i != min1)
min = i;
}
min2 = min;
}4、构建哈夫曼树
void CreateHuff(HuffmanTree& HT,double* w, int n)
{
int m = 2 * n - 1;
for (int i = 1; i <= n; i++)
{
HT[i].weight = w[i - 1];
}
for (int i = n + 1; i <= m; i++)
{
int min1, min2;
Select(HT, i - 1, min1, min2);
HT[i].weight = HT[min1].weight + HT[min2].weight;
HT[min1].parent = i;
HT[min2].parent = i;
HT[i].lc = min1;
HT[i].rc = min2;
}
printf("Huffman is: \n");
printf("subscript weight parent lchild rchild\n");
printf("0 \n");
for (int i = 1; i <= m; i++)
{
printf("%-4d %-6.2lf %-6d %-6d %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);
}
printf("\n");
}5、生成哈夫曼树编码
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{
HC = (HuffmanCode)malloc(sizeof(char*)*(n + 1));
char* code = (char*)malloc(sizeof(char)*n);
code[n - 1] = '\0';
for (int i = 1; i <= n; i++)
{
int start = n - 1;
int c = i;
int p = HT[c].parent;
while (p)
{
if (HT[p].lc == c)
code[--start] = '0';
else
code[--start] = '1';
c = p;
p = HT[c].parent;
}
HC[i] = (char*)malloc(sizeof(char)*(n - start));
strcpy(HC[i], &code[start]);
}
free(code);
}6、测试代码
void test()
{
int n = 0;
printf("input the number of data: ");
scanf("%d", &n);
double* w = (double*)malloc(sizeof(double)*n);
if (n >= 0)
{
printf("input the data: ");
for (int i = 0; i < n; i++)
{
scanf("%lf", &w[i]);
}
HuffmanTree HT;
HT = initHuffmanTree(HT,n);
CreateHuff(HT, w, n);
HuffmanCode HC;
HuffCoding(HT, HC, n);
for (int i = 1; i <= n; i++)
{
printf("The data %.2lf code is: %s\n", HT[i].weight, HC[i]);
}
free(w);
}
else
{
printf("malloc fail\n");
return;
}
}7、程序入口
int main()
{
test();
return 1;
}8、运行结果
input the number of data: 5
input the data: 0.1 0.2 0.3 0.25 0.15
Huffman is:
subscript weight parent lchild rchild
0
1 0.10 6 0 0
2 0.20 7 0 0
3 0.30 8 0 0
4 0.25 7 0 0
5 0.15 6 0 0
6 0.25 8 1 5
7 0.45 9 2 4
8 0.55 9 6 3
9 1.00 0 7 8
The data 0.10 code is: 100
The data 0.20 code is: 00
The data 0.30 code is: 11
The data 0.25 code is: 01
The data 0.15 code is: 101四、整体代码
#include <stdio.h>
#include <malloc.h>
#include <string.h>
typedef struct HTNode
{
double weight;
int parent;
int lc, rc;
}*HuffmanTree;
typedef char **HuffmanCode;
HuffmanTree initHuffmanTree(HuffmanTree& HT,int n)
{
int i;
int m = 2 * n - 1;
HT = (HuffmanTree)malloc(sizeof(HTNode)*(m + 1));
for(i = 0; i <= m; i++)
{
HT[i].lc = 0;
HT[i].parent = 0;
HT[i].rc = 0;
HT[i].weight = 0;
}
return HT;
}
void Select(HuffmanTree& HT, int n, int& min1, int& min2)
{
int min;
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0)
{
min = i;
break;
}
}
for (int i = min + 1; i <= n; i++)
{
if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)
min = i;
}
min1 = min;
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0 && i != min1)
{
min = i;
break;
}
}
for (int i = min + 1; i <= n; i++)
{
if (HT[i].parent == 0 && HT[i].weight < HT[min].weight&&i != min1)
min = i;
}
min2 = min;
}
void CreateHuff(HuffmanTree& HT,double* w, int n)
{
int m = 2 * n - 1;
for (int i = 1; i <= n; i++)
{
HT[i].weight = w[i - 1];
}
for (int i = n + 1; i <= m; i++)
{
int min1, min2;
Select(HT, i - 1, min1, min2);
HT[i].weight = HT[min1].weight + HT[min2].weight;
HT[min1].parent = i;
HT[min2].parent = i;
HT[i].lc = min1;
HT[i].rc = min2;
}
printf("Huffman is: \n");
printf("subscript weight parent lchild rchild\n");
printf("0 \n");
for (int i = 1; i <= m; i++)
{
printf("%-4d %-6.2lf %-6d %-6d %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);
}
printf("\n");
}
void HuffCoding(HuffmanTree& HT, HuffmanCode& HC, int n)
{
HC = (HuffmanCode)malloc(sizeof(char*)*(n + 1));
char* code = (char*)malloc(sizeof(char)*n);
code[n - 1] = '\0';
for (int i = 1; i <= n; i++)
{
int start = n - 1;
int c = i;
int p = HT[c].parent;
while (p)
{
if (HT[p].lc == c)
code[--start] = '0';
else
code[--start] = '1';
c = p;
p = HT[c].parent;
}
HC[i] = (char*)malloc(sizeof(char)*(n - start));
strcpy(HC[i], &code[start]);
}
free(code);
}
void test()
{
int n = 0;
printf("input the number of data: ");
scanf("%d", &n);
double* w = (double*)malloc(sizeof(double)*n);
if (n >= 0)
{
printf("input the data: ");
for (int i = 0; i < n; i++)
{
scanf("%lf", &w[i]);
}
HuffmanTree HT;
HT = initHuffmanTree(HT,n);
CreateHuff(HT, w, n);
HuffmanCode HC;
HuffCoding(HT, HC, n);
for (int i = 1; i <= n; i++)
{
printf("The data %.2lf code is: %s\n", HT[i].weight, HC[i]);
}
free(w);
}
else
{
printf("malloc fail\n");
return;
}
}
int main()
{
test();
return 1;
}