使用 LSTM 进行多变量时间序列预测

我们先来了解两个主题：

• 什么是时间序列分析？

• 什么是 LSTM？

时间序列分析：时间序列表示基于时间顺序的一系列数据。它可以是秒、分钟、小时、天、周、月、年。未来的数据将取决于它以前的值。

在现实世界的案例中，我们主要有两种类型的时间序列分析：

• 单变量时间序列

• 多元时间序列

对于单变量时间序列数据，我们将使用单列进行预测。

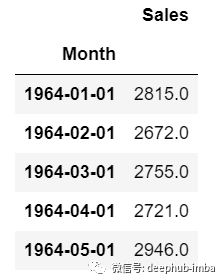
正如我们所见，只有一列，因此即将到来的未来值将仅取决于它之前的值。

但是在多元时间序列数据的情况下，将有不同类型的特征值并且目标数据将依赖于这些特征。

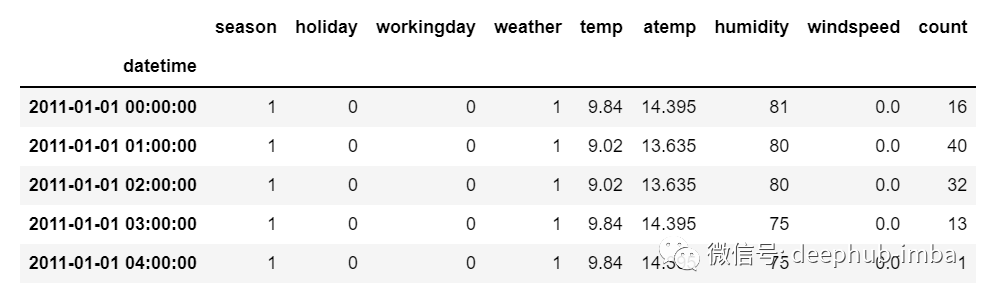
正如在图片中看到的，在多元变量中将有多个列来对目标值进行预测。（上图中“count”为目标值）

在上面的数据中，count不仅取决于它以前的值，还取决于其他特征。因此，要预测即将到来的count值，我们必须考虑包括目标列在内的所有列来对目标值进行预测。

在执行多元时间序列分析时必须记住一件事，我们需要使用多个特征预测当前的目标，让我们通过一个例子来理解：

在训练时，如果我们使用 5 列 [feature1, feature2, feature3, feature4, target] 来训练模型，我们需要为即将到来的预测日提供 4 列 [feature1, feature2, feature3, feature4]。

LSTM

本文中不打算详细讨论LSTM。所以只提供一些简单的描述，如果你对LSTM没有太多的了解，可以参考我们以前发布的文章。

LSTM基本上是一个循环神经网络，能够处理长期依赖关系。

假设你在看一部电影。所以当电影中发生任何情况时，你都已经知道之前发生了什么，并且可以理解因为过去发生的事情所以才会有新的情况发生。RNN也是以同样的方式工作，它们记住过去的信息并使用它来处理当前的输入。RNN的问题是，由于渐变消失，它们不能记住长期依赖关系。因此为了避免长期依赖问题设计了lstm。

现在我们讨论了时间序列预测和LSTM理论部分。让我们开始编码。

让我们首先导入进行预测所需的库：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM
from tensorflow.keras.layers import Dense, Dropout
from sklearn.preprocessing import MinMaxScaler
from keras.wrappers.scikit_learn import KerasRegressor
from sklearn.model_selection import GridSearchCV

加载数据，并检查输出：

df=pd.read_csv("train.csv",parse_dates=["Date"],index_col=[0])df.head()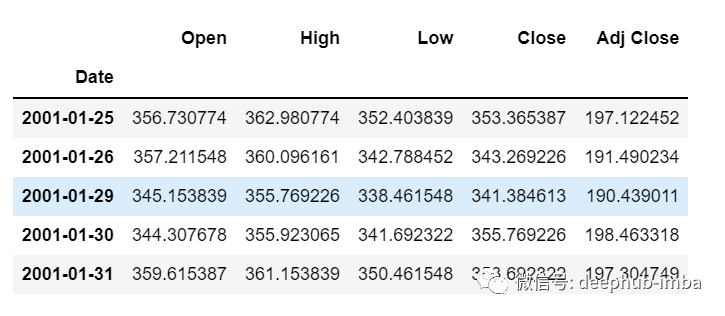

df.tail()

现在让我们花点时间看看数据：csv文件中包含了谷歌从2001-01-25到2021-09-29的股票数据，数据是按照天数频率的。

[如果您愿意，您可以将频率转换为“B”[工作日]或“D”，因为我们不会使用日期，我只是保持它的现状。]

这里我们试图预测“Open”列的未来值，因此“Open”是这里的目标列。

让我们看一下数据的形状：

df.shape(5203,5)

现在让我们进行训练测试拆分。这里我们不能打乱数据，因为在时间序列中必须是顺序的。

test_split=round(len(df)*0.20)
df_for_training=df[:-1041]
df_for_testing=df[-1041:]
print(df_for_training.shape)
print(df_for_testing.shape)
(4162, 5)(1041, 5)

可以注意到数据范围非常大，并且它们没有在相同的范围内缩放，因此为了避免预测错误，让我们先使用MinMaxScaler缩放数据。(也可以使用StandardScaler)

scaler = MinMaxScaler(feature_range=(0,1))
df_for_training_scaled = scaler.fit_transform(df_for_training)
df_for_testing_scaled=scaler.transform(df_for_testing)
df_for_training_scaled

将数据拆分为X和Y，这是最重要的部分，正确阅读每一个步骤。

def createXY(dataset,n_past):
  dataX = []
  dataY = []
  for i in range(n_past, len(dataset)):
          dataX.append(dataset[i - n_past:i, 0:dataset.shape[1]])
          dataY.append(dataset[i,0])
  return np.array(dataX),np.array(dataY)

trainX,trainY=createXY(df_for_training_scaled,30)
testX,testY=createXY(df_for_testing_scaled,30)

让我们看看上面的代码中做了什么：

N_past是我们在预测下一个目标值时将在过去查看的步骤数。

这里使用30，意味着将使用过去的30个值(包括目标列在内的所有特性)来预测第31个目标值。

因此，在trainX中我们会有所有的特征值，而在trainY中我们只有目标值。

让我们分解for循环的每一部分：

对于训练，dataset = df_for_training_scaled, n_past=30

当i= 30：

data_X.addend (df_for_training_scaled[i - n_past:i, 0:df_for_training.shape[1]])

从n_past开始的范围是30，所以第一次数据范围将是-[30 - 30,30,0:5] 相当于 [0:30,0:5]

因此在dataX列表中，df_for_training_scaled[0:30,0:5]数组将第一次出现。

现在, dataY.append(df_for_training_scaled[i,0])

i = 30，所以它将只取第30行开始的open(因为在预测中，我们只需要open列，所以列范围仅为0，表示open列)。

第一次在dataY列表中存储df_for_training_scaled[30,0]值。

所以包含5列的前30行存储在dataX中，只有open列的第31行存储在dataY中。然后我们将dataX和dataY列表转换为数组，它们以数组格式在LSTM中进行训练。

我们来看看形状。

print("trainX Shape-- ",trainX.shape)
print("trainY Shape-- ",trainY.shape)

(4132, 30, 5)
(4132,)

print("testX Shape-- ",testX.shape)
print("testY Shape-- ",testY.shape)

(1011, 30, 5)
(1011,)

4132 是 trainX 中可用的数组总数，每个数组共有 30 行和 5 列， 在每个数组的 trainY 中，我们都有下一个目标值来训练模型。

让我们看一下包含来自 trainX 的 (30,5) 数据的数组之一 和 trainX 数组的 trainY 值：

print("trainX[0]-- \n",trainX[0])
print("trainY[0]-- ",trainY[0])

如果查看 trainX[1] 值，会发现到它与 trainX[0] 中的数据相同（第一列除外），因为我们将看到前 30 个来预测第 31 列，在第一次预测之后它会自动移动 到第 2 列并取下一个 30 值来预测下一个目标值。

让我们用一种简单的格式来解释这一切：

trainX — — →trainY

[0 : 30,0:5] → [30,0]

[1:31, 0:5] → [31,0]

[2:32,0:5] →[32,0]

像这样，每个数据都将保存在 trainX 和 trainY 中。

现在让我们训练模型，我使用 girdsearchCV 进行一些超参数调整以找到基础模型。

def build_model(optimizer):
  grid_model = Sequential()
  grid_model.add(LSTM(50,return_sequences=True,input_shape=(30,5)))
  grid_model.add(LSTM(50))
  grid_model.add(Dropout(0.2))
  grid_model.add(Dense(1))

grid_model.compile(loss = 'mse',optimizer = optimizer)
  return grid_modelgrid_model = KerasRegressor(build_fn=build_model,verbose=1,validation_data=(testX,testY))

parameters = {'batch_size' : [16,20],
            'epochs' : [8,10],
            'optimizer' : ['adam','Adadelta'] }

grid_search = GridSearchCV(estimator = grid_model,
                          param_grid = parameters,
                          cv = 2)

如果你想为你的模型做更多的超参数调整，也可以添加更多的层。但是如果数据集非常大建议增加 LSTM 模型中的时期和单位。

在第一个 LSTM 层中看到输入形状为 (30,5)。它来自 trainX 形状。

(trainX.shape[1],trainX.shape[2]) → (30,5)

现在让我们将模型拟合到 trainX 和 trainY 数据中。

grid_search = grid_search.fit(trainX,trainY)

由于进行了超参数搜索，所以这将需要一些时间来运行。

你可以看到损失会像这样减少：

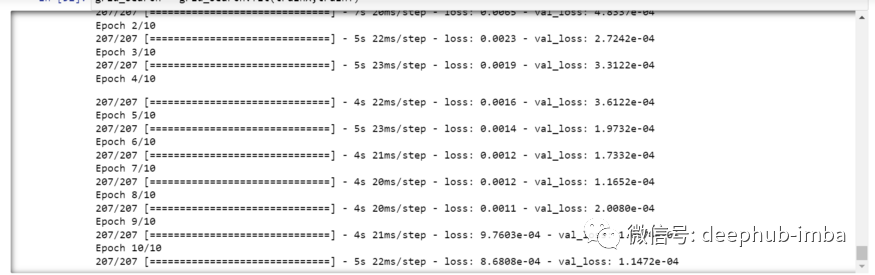
现在让我们检查模型的最佳参数。

grid_search.best_params_{‘batch_size’: 20, ‘epochs’: 10, ‘optimizer’: ‘adam’}

将最佳模型保存在 my_model 变量中。

my_model=grid_search.best_estimator_.model

现在可以用测试数据集测试模型。

prediction=my_model.predict(testX)print("prediction\n", prediction)
print("\nPrediction Shape-",prediction.shape)

testY 和 prediction 的长度是一样的。现在可以将 testY 与预测进行比较。

但是我们一开始就对数据进行了缩放，所以首先我们必须做一些逆缩放过程。​​​​​​​

scaler.inverse_transform(prediction)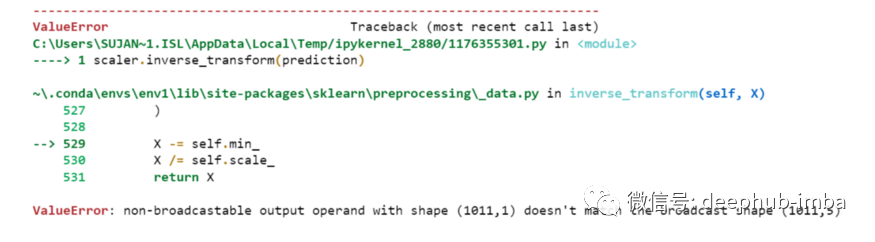

报错了，这是因为在缩放数据时，我们每行有 5 列，现在我们只有 1 列是目标列。

所以我们必须改变形状来使用 inverse_transform：​​​​​​​

prediction_copies_array = np.repeat(prediction,5, axis=-1)

5 列值是相似的，它只是将单个预测列复制了 4 次。所以现在我们有 5 列相同的值 。​​​​​​​

prediction_copies_array.shape(1011,5)

这样就可以使用 inverse_transform 函数。

pred=scaler.inverse_transform(np.reshape(prediction_copies_array,(len(prediction),5)))[:,0]

但是逆变换后的第一列是我们需要的，所以我们在最后使用了 → [:,0]。

现在将这个 pred 值与 testY 进行比较，但是 testY 也是按比例缩放的，也需要使用与上述相同的代码进行逆变换。

original_copies_array = np.repeat(testY,5, axis=-1)
original=scaler.inverse_transform(np.reshape(original_copies_array,(len(testY),5)))[:,0]

现在让我们看一下预测值和原始值：

print("Pred Values-- " ,pred)
print("\nOriginal Values-- " ,original)

最后绘制一个图来对比我们的 pred 和原始数据。

plt.plot(original, color = 'red', label = 'Real Stock Price')
plt.plot(pred, color = 'blue', label = 'Predicted Stock Price')
plt.title('Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Google Stock Price')
plt.legend()plt.show()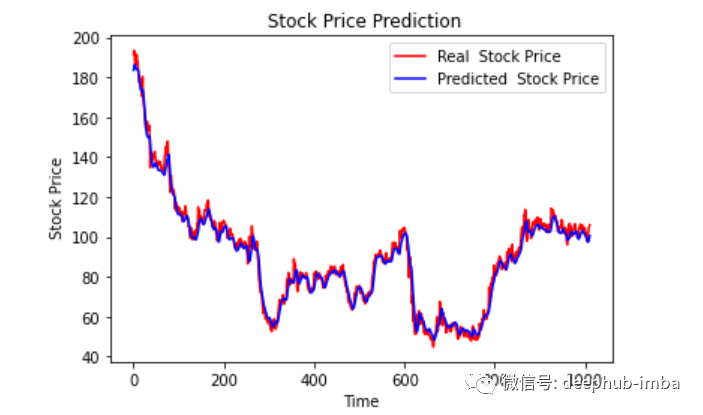

看样子还不错，到目前为止，我们训练了模型并用测试值检查了该模型。现在让我们预测一些未来值。

从主 df 数据集中获取我们在开始时加载的最后 30 个值[为什么是 30？因为这是我们想要的过去值的数量，来预测第 31 个值]

df_30_days_past=df.iloc[-30:,:]df_30_days_past.tail()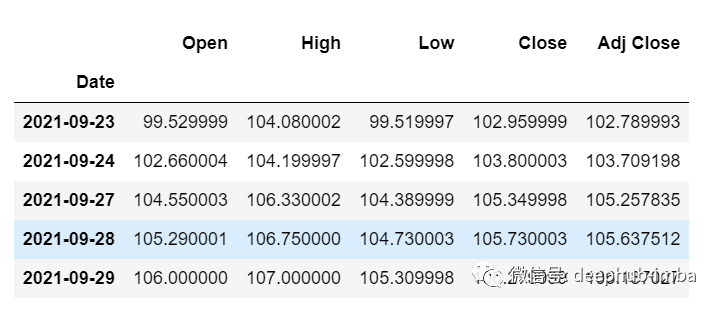

可以看到有包括目标列（“Open”）在内的所有列。现在让我们预测未来的 30 个值。

在多元时间序列预测中，需要通过使用不同的特征来预测单列，所以在进行预测时我们需要使用特征值（目标列除外）来进行即将到来的预测。

这里我们需要“High”、“Low”、“Close”、“Adj Close”列的即将到来的 30 个值来对“Open”列进行预测。​​​

df_30_days_future=pd.read_csv("test.csv",parse_dates=["Date"],index_col=[0])df_30_days_future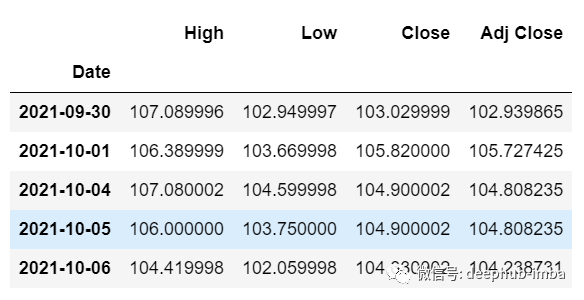

剔除“Open”列后，使用模型进行预测之前还需要做以下的操作：

缩放数据，因为删除了‘Open’列，在缩放它之前，添加一个所有值都为“0”的Open列。

缩放后，将未来数据中的“Open”列值替换为“nan”

现在附加 30 天旧值和 30 天新值（其中最后 30 个“打开”值是 nan）

df_30_days_future["Open"]=0
df_30_days_future=df_30_days_future[["Open","High","Low","Close","Adj Close"]]
old_scaled_array=scaler.transform(df_30_days_past)
new_scaled_array=scaler.transform(df_30_days_future)
new_scaled_df=pd.DataFrame(new_scaled_array)
new_scaled_df.iloc[:,0]=np.nan
full_df=pd.concat([pd.DataFrame(old_scaled_array),new_scaled_df]).reset_index().drop(["index"],axis=1)

full_df  形状是 (60,5)，最后第一列有 30 个 nan 值。

要进行预测必须再次使用 for 循环，我们在拆分 trainX 和 trainY 中的数据时所做的。但是这次我们只有 X，没有 Y 值。

full_df_scaled_array=full_df.values
all_data=[]
time_step=30
for i in range(time_step,len(full_df_scaled_array)):
  data_x=[]
  data_x.append(
    full_df_scaled_array[i-time_step :i , 0:full_df_scaled_array.shape[1]])
  data_x=np.array(data_x)
  prediction=my_model.predict(data_x)
  all_data.append(prediction)
  full_df.iloc[i,0]=prediction

对于第一个预测，有之前的 30 个值，当 for 循环第一次运行时它会检查前 30 个值并预测第 31 个“Open”数据。

当第二个 for 循环将尝试运行时，它将跳过第一行并尝试获取下 30 个值 [1:31] 。这里会报错错误因为Open列最后一行是 “nan”，所以需要每次都用预测替换“nan”。

最后还需要对预测进行逆变换：

new_array=np.array(all_data)
new_array=new_array.reshape(-1,1)
prediction_copies_array = np.repeat(new_array,5, axis=-1)
y_pred_future_30_days = scaler.inverse_transform(np.reshape(prediction_copies_array,(len(new_array),5)))[:,0]
print(y_pred_future_30_days)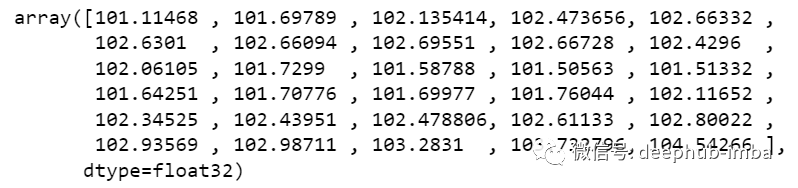

这样一个完整的流程就已经跑通了。

如果你想看完整的代码，可以在这里查看：

https://github.com/sksujan58/Multivariate-time-series-forecasting-using-LSTM