数据结构(一)——概述

一、绪论

1.1数据结构的基本概念

数据：用来描述客观事物的数、计算机中是字符及所有能输入并被程序识别和处理的符号的集合。

数据元素：数据的基本单位，一个数据元素可由若干数据项组成。

数据结构：指相互之间存在一种或多种特定关系的数据元素的集合。
数据结构的三要素：逻辑结构、存储结构、数据的运算。

数据对象：具有相同性质的数据元素的集合，是数据的一个子集。

逻辑结构：指数据元素之间的逻辑关系

  • 集合：各个元素同属一个集合，别无其它关系。
  • 线性结构：数据元素之间是一对一的关系。
  • 树型结构：数据元素之间是一对多的关系。
  • 图状结构（网状结构）：数据元素之间存在多对多的关系。

存储结构(物理结构)：用计算机表示数据元素的逻辑关系（后三种统称为非顺序存储)

  • 顺序存储：把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。
  • 链式存储：逻辑上相邻的元素在物理位置上可以不相邻，可借助指示元素存储地址的指针来表示元素之间的逻辑关系。
  • 索引存储：在存储元素信息的同时，建立附加的索引表。索引表中的每项称为索引项，索引项 的一般形式是（关键字，地址）。
  • 散列存储：根据元素的关键字直接计算出该元素的存储地址，又称哈希（Hash）存储。
  1. 若采用顺序存储，则各个数据元素在物理上必须是连续的；
    若采用非顺序存储，则各个数据元素在物理上可以是离散的。
  2. 数据的存储结构会影响存储空间分配的方便程度
  3. 数据的存储结构会影响对数据运算的速度

数据的运算：运算的定义是针对逻辑结构的， 指出运算的功能；运算的实现是针对存储结构的，指出运算的具体操作步骤。
例：结合现实需求定义队列这种逻辑结构的运算：
①队头元素出队； ②新元素入队； ③输出队列长度；

数据类型：数据类型是一个值的集合和定义在此集合上的一组操作的总称。
   1）原子类型。其值不可再分的数据类型
   2）结构类型。其值可以再分解为若干成分（分量）的数据类型

抽象数据类型（ADT）：是抽象数据组织及与之相关的操作。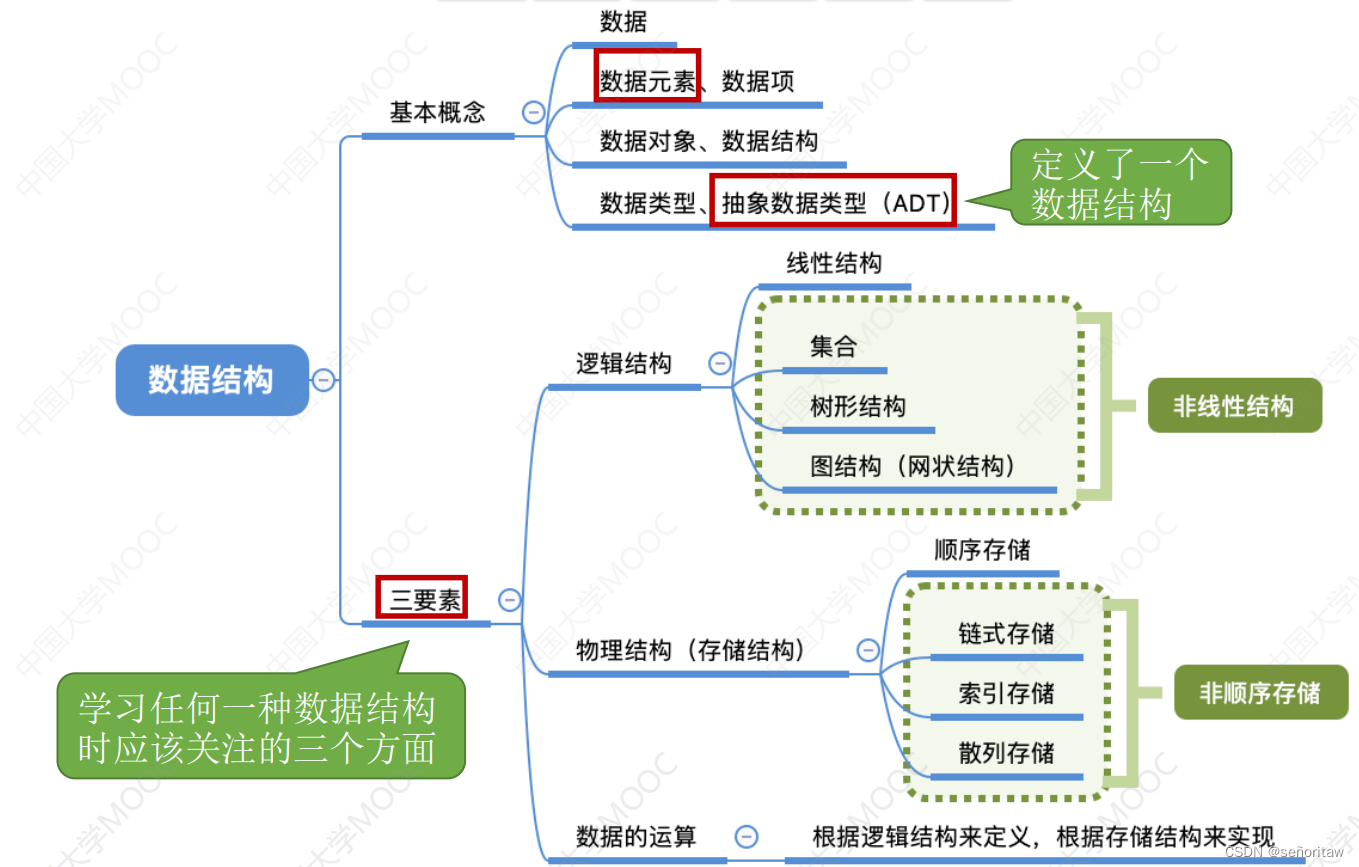
​

1.2算法和算法评价

1.2.1 算法的基本概念

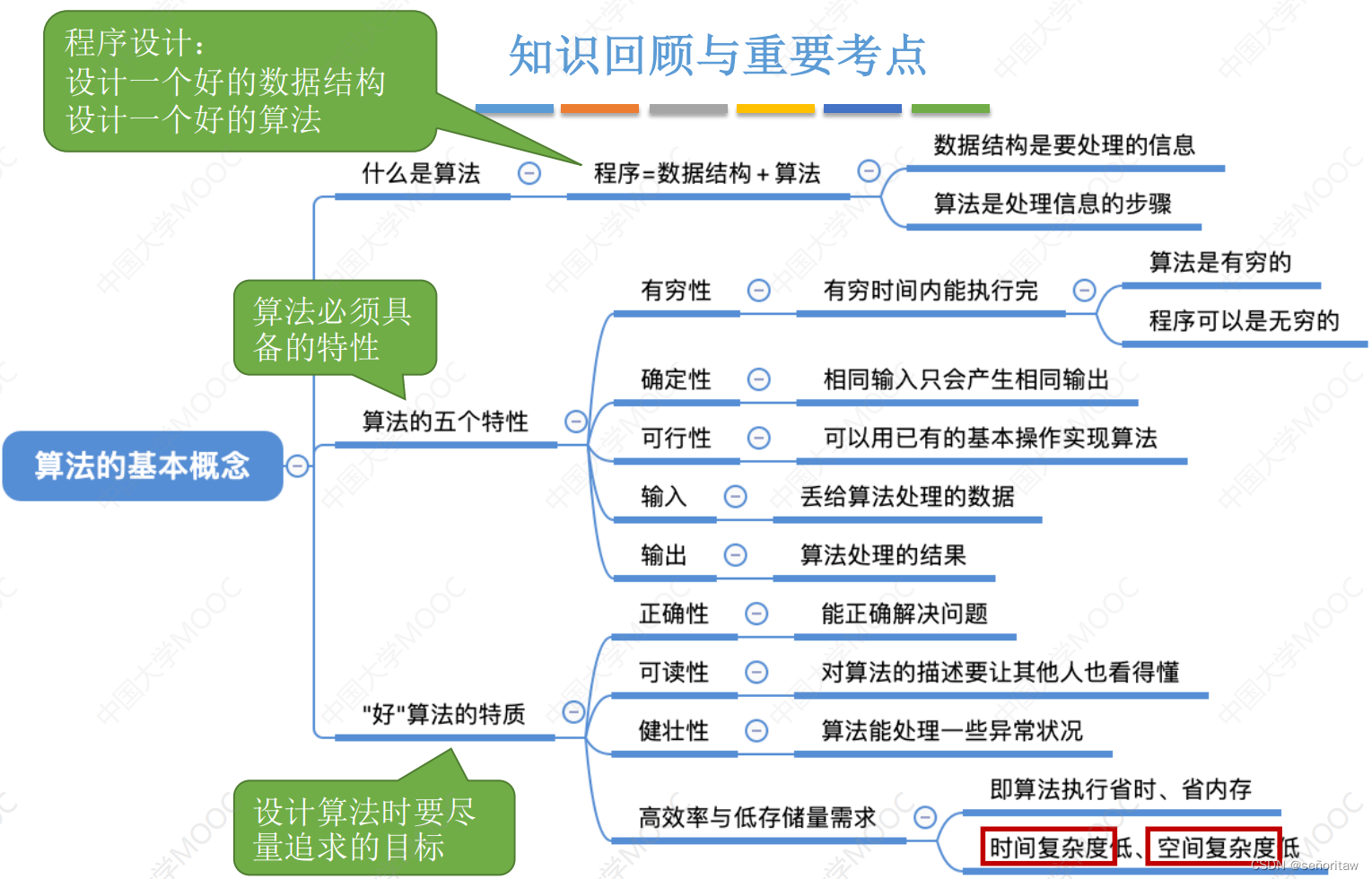
算法：对特定问题求解步骤的一种描述，是指令的有限序列。其中的每条指令表示一个或多个操作

算法的特性：有穷性、确定性、可行性、输入、输出。

  • 有穷性：一个算法必须总在执行有穷步之后结束，且每一步都可在有穷时间内完成。
    用有限步骤解决某个特定的问题
  • 确定性：算法中每条指令必须有确切的含义，对于相同的输入只能得出相同的输出。
  • 可行性：算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
  • 输入：一个算法有零个或多个输入，这些输入取自于某个特定的对象的集合。
  • 输出：一个算法有一个或多个输出，这些输出是与输入有着某种特定关系的量。

算法的设计目标：正确性，可读性，健壮性，高效率与低存储量需求。

  • 正确性。算法应能够正确地解决求解问题。
  • 可读性。算法应具有良好的可读性，以帮助人们理解
  • 健壮性。输入非法数据时算法能适当地做出反应或进行处理，而不会产生莫名其妙的输出结果
  • 高效率与低存储量需求。花费时间少时间复杂度低；不费内存，空间复杂度低。

1.2.2 算法的时间复杂度

算法时间复杂度：事前预估算法时间开销T(n)与问题规模 n 的关系（T 表示 “time）.

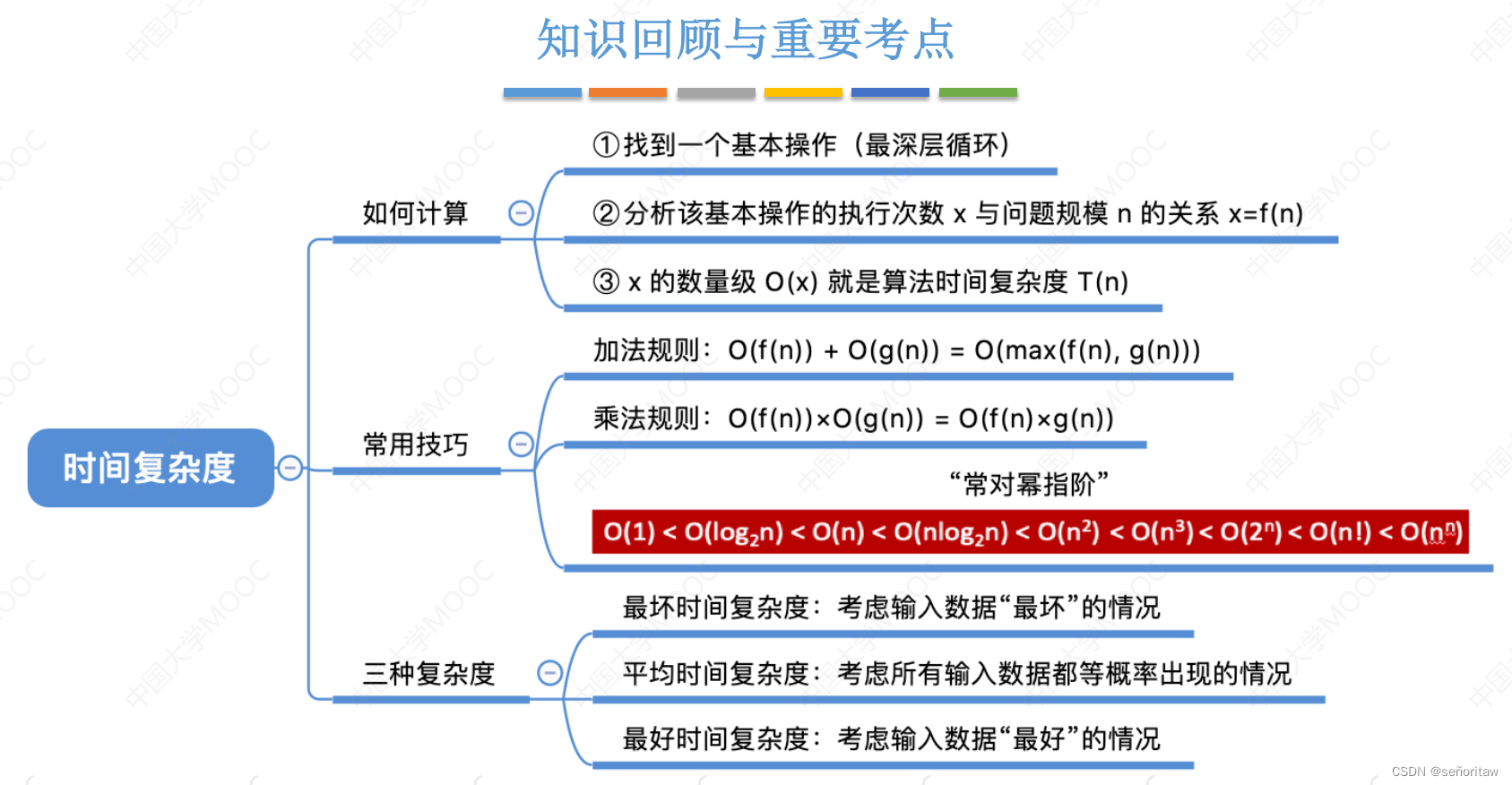
如何计算：

  1. 找到一个基本操作（最深层循环)
  2. 分析该基本操作的执行次数x与问题规模n的关系x=f(n)
  3. x的数量级O(x)就是算法时间复杂度T (n)

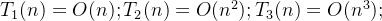
  T_{1}(n) = O(n); T_{2}(n) = O(n^{2}); T_{3}(n) = O(n^{3});

  大O表示“同阶”，同等数量级，即当n→∞时，二者之比为常数。

  结论：可以只考虑阶数高的部分,问题规模足够大时，常数项系数也可以忽略。

  常用技巧：

  a）加法规则

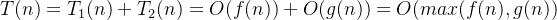
  T(n) = T_{1}(n) + T_{2}(n) = O(f(n)) + O(g(n)) = O(max(f(n), g(n))
  多项相加，只保留最高阶的项，且系数变为1

  b）乘法规则

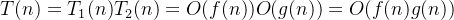
  T(n) = T_{1}(n)×T_{2}(n) = O(f(n))×O(g(n)) = O(f(n)×g(n))
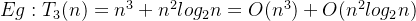
  Eg:T_{3}(n)= n^{3}+ n^{2} log_{2}n = O( n^{3}) + O(n^{2} log_{2}n)
  多项相乘，都保留

   c）“常对幂指阶”  常数级<对数级<幂函数级<指数级<阶层级

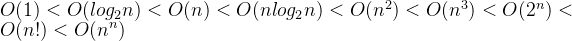
   O(1) < O(log_{2}n) < O(n) < O(nlog_{2}n) < O(n^{2}) < O(n^{3}) < O(2^{n}) < O(n!) < O(n^{n})

三种时间复杂度:

  1. 最坏时间复杂度：最坏情况下算法的时间复杂度
  2. 平均时间复杂度：所有输入示例等概率出现的情况下，算法的期望运行时间
  3. 最好时间复杂度：最好情况下算法的时间复杂度 （一般不考虑）

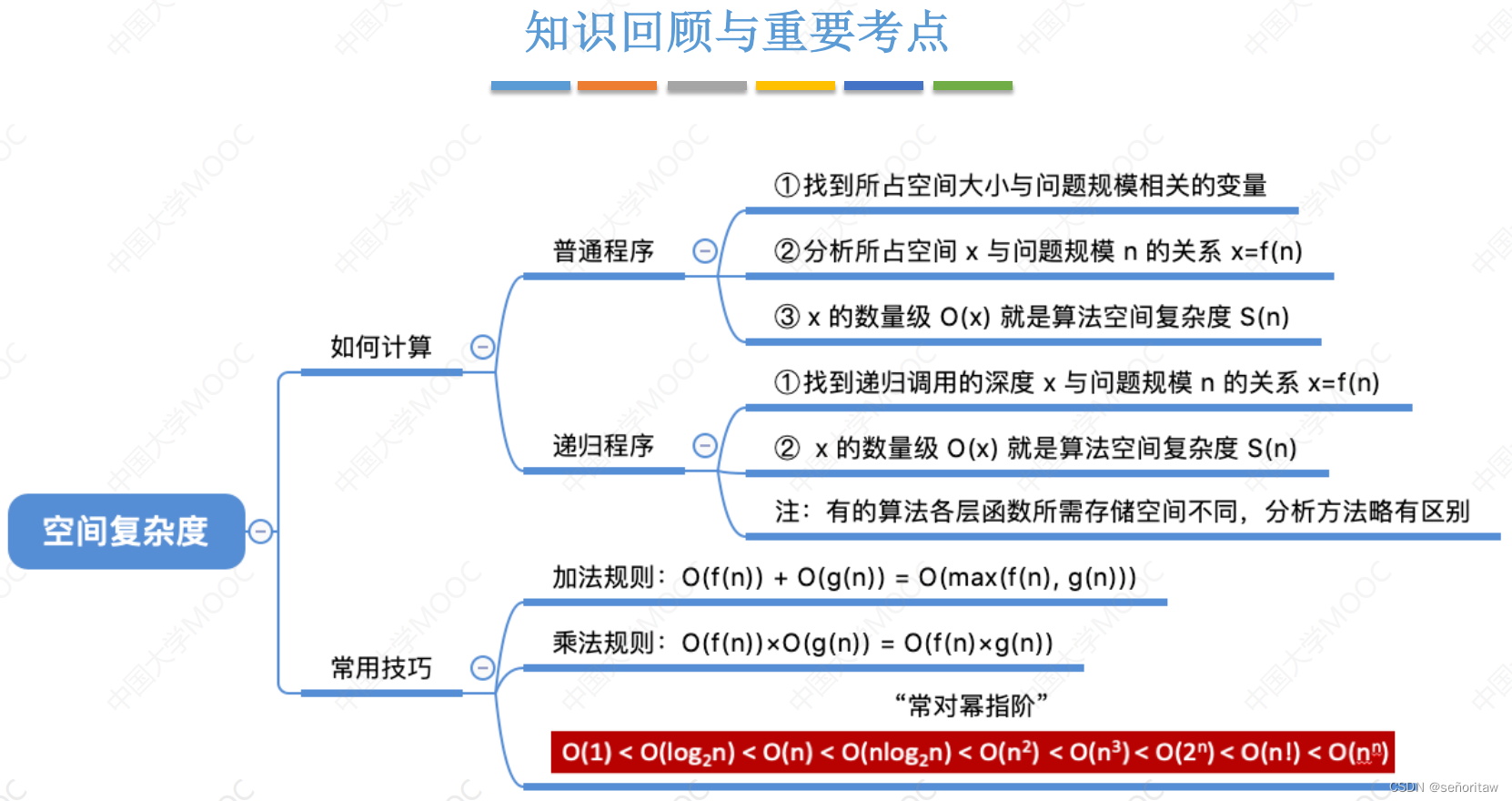
1.2.3 算法的空间复杂度