音乐指纹识别(三):波形特征
对主流的音频格式进行解析以后,绘制出了声音的波形。一段音频的特征,需要在这段波形中寻找。在这里,会用到一些基础的数学知识,在文中只是简略的用文字进行原理的说明。
在数学中有提到,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。这段话如果用不太严谨语言,可以这样来理解,对一段的曲线来说,我们都可以用一组正弦曲线和余弦曲线叠加而成。这样一来,曲线就分解为一个一个正弦曲线和余弦曲线的叠加,只要知道主要的正弦和余弦曲线,就能够来表示这一段曲线的特征。
那正弦和余弦我们这么能够来表示曲线的特征呢?
在正弦和余弦中,每一条正弦和余弦都有自己的振幅和频率,振幅和频率就能代表正弦或者余弦的特征。
还有一个问题是需要有无穷多的正弦和余弦来拟合这条曲线,那特征不也是无效多个,在这里我们只取振幅较大的正余弦,也就是这几条正余弦主要构成了这条曲线,这是问题的主因。
寻找曲线的特征变成了选择构成主要正余弦的频率。
在工程中,有时域和频域的不同表示,现在我们需要频率的东西,需要把时域转换到频域中,转换的方法为傅里叶变换。
在实验中,先模拟一条曲线,在通过曲线的数据进行傅里叶变换后,看看能得到什么样的图形。
# -*- coding:utf-8 -*-
# /usr/bin/python2.7
import numpy as np
from scipy.fftpack import fft,ifft
import matplotlib.pyplot as plt
import seaborn
from matplotlib.font_manager import FontProperties
import pylab as pl
import numpy as np
sampling_rate = 8000
fft_size = 512
# 156.25和234.375HZ组成的曲线
t = np.arange(0, 1.0, 1.0/sampling_rate)
x = np.sin(2*np.pi*156.25*t) + 2*np.sin(2*np.pi*234.375*t)
xs = x[:fft_size]
#进行傅里叶变换
xf = np.fft.rfft(xs)/fft_size
freqs = np.linspace(0, sampling_rate/2, fft_size/2+1)
#归一
xfp = 20*np.log10(np.clip(np.abs(xf), 1e-20, 1e100))
#绘制时域和频域的图片
pl.figure(figsize=(8,4))
pl.subplot(211)
pl.plot(t[:fft_size], xs)
pl.xlabel(u"s")
pl.title(u"156.25Hz 234.375Hz")
pl.subplot(212)
pl.plot(freqs, xfp)
pl.xlabel(u"Hz")
pl.subplots_adjust(hspace=0.4)
pl.show()
图片如下:
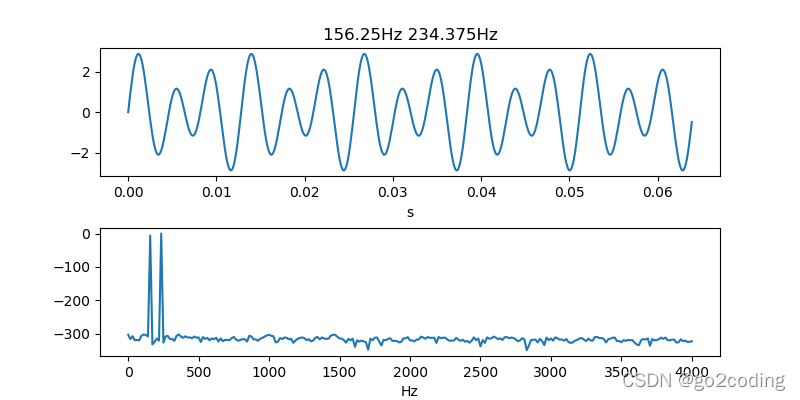
在代码中,使用156.25和234.375HZ的正弦组成了一条有周期的曲线,通过傅里叶变换后发现在156.25和234.375HZ的振幅最大,也就是由这两条正弦组成了这条曲线。
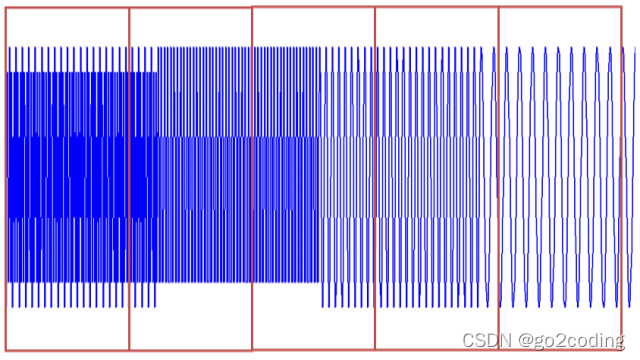
还有一个问题是一开始我们是假设这条曲线是周期性的,但有时候而且是更经常的时候波形的频率是变化的。如下图可以看出。
这时候需要采用的是傅里叶的另一种形式,成为短时傅里叶变换。可以把短时傅里叶变换理解为按时间分段的进行傅里叶变换。
可以通过如下的模拟,更能体现出短时傅里叶变换 的用法。
# -*- coding:utf-8 -*-
# /usr/bin/python2.7
import matplotlib.pyplot as plt
import numpy as np
# Fixing random state for reproducibility
np.random.seed(19680801)
dt = 0.0005
t = np.arange(0.0, 20.0, dt)
s1 = np.sin(2 * np.pi * 100 * t)
s2 = 2 * np.sin(2 * np.pi * 400 * t)
# create a transient "chirp"
mask = np.where(np.logical_and(t > 10, t < 12), 1.0, 0.0)
s2 = s2 * mask
# add some noise into the mix
nse = 0.01 * np.random.random(size=len(t))
x = s1 + s2 + nse # the signal
NFFT = 1024 # the length of the windowing segments
Fs = int(1.0 / dt) # the sampling frequency
fig, (ax1, ax2) = plt.subplots(nrows=2)
ax1.plot(t, x)
Pxx, freqs, bins, im = ax2.specgram(x, NFFT=NFFT, Fs=Fs, noverlap=900)
# The `specgram` method returns 4 objects. They are:
# - Pxx: the periodogram
# - freqs: the frequency vector
# - bins: the centers of the time bins
# - im: the matplotlib.image.AxesImage instance representing the data in the plot
plt.show()
代码对s2 信号进行了处理在10 和 12之间存在数据,总的信号如果直接要用傅里叶变换,s2 信号自然会被削弱,看看短时傅里叶变换 的波形:
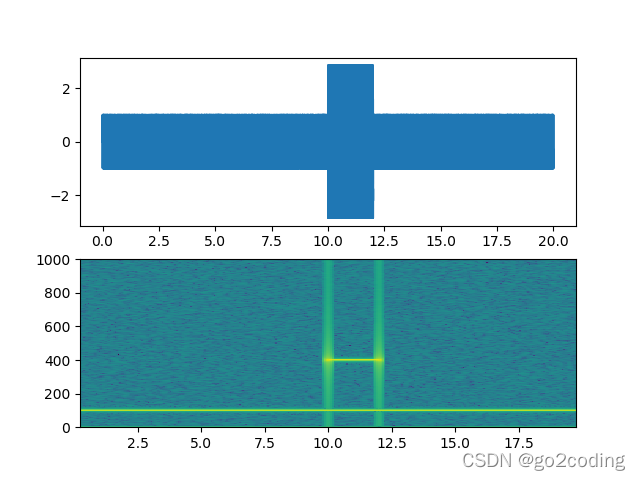
可以看出100Hz 的频率不管在什么时候都是存在的,而400Hz 的在10 和 12之间才出现,这能更好的拟合现实的情况。