编译原理基本定义(文法、算符文法、算符优先文法、算符优先关系表、算符优先分析过程)
文法
文法和语言分为4类。
0型文法:最大类,包含1、2、3型文法。
1型文法:对0型文法来说,所有的产生式的右边的字符长度都要大于左边的字符长度。
2型文法:所有的产生式左边都只有一个字符。
3型文法:在满足2型文法的基础上,每个产生式具有以下形式:A–>a(终结符)、A–>a(终结符)B(非终结符),或者具有以下形式:A–>a(终结符)、A–>B(非终结符)a(终结符)。
例:
S–>aS
S–>aA
A–>bA
A–>bB
B–>cB
B–>c
这个就是3型文法。
但是
S–>aS
S–>aA
A–>bA
A–>bB
A–>Ac
就不是3型文法,因为它既是左线性,又是右线性。
算符优先文法
算符文法:任何产生式的右部都不含两个相邻的非终结符。
定义算符优先文法之前先定义终结符的关系。
在产生式中,如果R–>…ab…或者R–>…aQb…,那么这两个终结符a和b的关系为:a=b,等于号中间还有个点,但是不知道怎么打上去,所以后面都用等号来代替书上的符号。
在产生式中,如果R–>…aQ…,然后又有Q–>b…或者Q–>Cb…这样的情况存在,那么这两个终结符a和b的关系为:a<b,小于号中间还有个点,所以后面都用小于号来代替书上的符号。
在产生式中,如果R–>…Qb…,然后又有Q–>…a或者Q–>…aC这样的情况存在,那么这两个终结符a和b的关系为:a>b,大于号中间还有个点,所以后面都用大于号来代替书上的符号。
其实终结符的关系,画出语法树就很容易看出来,如果一个终结符的深度大于另一个终结符的深度,那么很可能就是深度越深的那个终结符关系大于深度较浅的终结符关系。后面我们定义了FIRSTVT和LASTVT就很容易求得并理解这些关系了。
算符优先文法:满足算符文法的情况下,任意一对终结符的关系(a,b)最多只有一种情况。
如何求一个非终结符的FIRSTVT?
很简单,对于一个非终结符T来说,有产生式是这样的T–>Qa…或者T–>a…,那么就有
F
I
R
S
T
V
T
(
T
)
=
{
a
}
集
合
并
上
F
I
R
S
T
V
T
(
Q
)
FIRSTVT(T)=\{a\}集合并上FIRSTVT(Q)
FIRSTVT(T)={a}集合并上FIRSTVT(Q),即如果
F
I
R
S
T
V
T
(
Q
)
=
{
b
,
c
}
FIRSTVT(Q)=\{b,c\}
FIRSTVT(Q)={b,c},那么就有
F
I
R
S
T
V
T
(
T
)
=
{
a
,
b
,
c
}
FIRSTVT(T)=\{a,b,c\}
FIRSTVT(T)={a,b,c}
如何求一个非终结符的LASTVT?
很简单,对于一个非终结符T来说,有产生式是这样的T–>…a或者T–>…aQ,那么就有
L
A
S
T
V
T
(
T
)
=
{
a
}
集
合
并
上
L
A
S
T
V
T
(
Q
)
LASTVT(T)=\{a\}集合并上LASTVT(Q)
LASTVT(T)={a}集合并上LASTVT(Q),即如果
L
A
S
T
V
T
(
Q
)
=
{
b
,
c
}
LASTVT(Q)=\{b,c\}
LASTVT(Q)={b,c},那么就有
L
A
S
T
V
T
(
T
)
=
{
a
,
b
,
c
}
LASTVT(T)=\{a,b,c\}
LASTVT(T)={a,b,c}
然后我们可以根据FIRSTVT和LASTVT求得算符优先关系表。
第一步:求出所有非终结符的FIRSTVT和LASTVT。
第二步:找出所有的产生式,然后根据上面的规则求得所有终结符的关系。
第四步:对额外的语句#S#,进行求解关系。其中S是起始非终结符。
第三步:构建算符优先关系表。如下的样子:
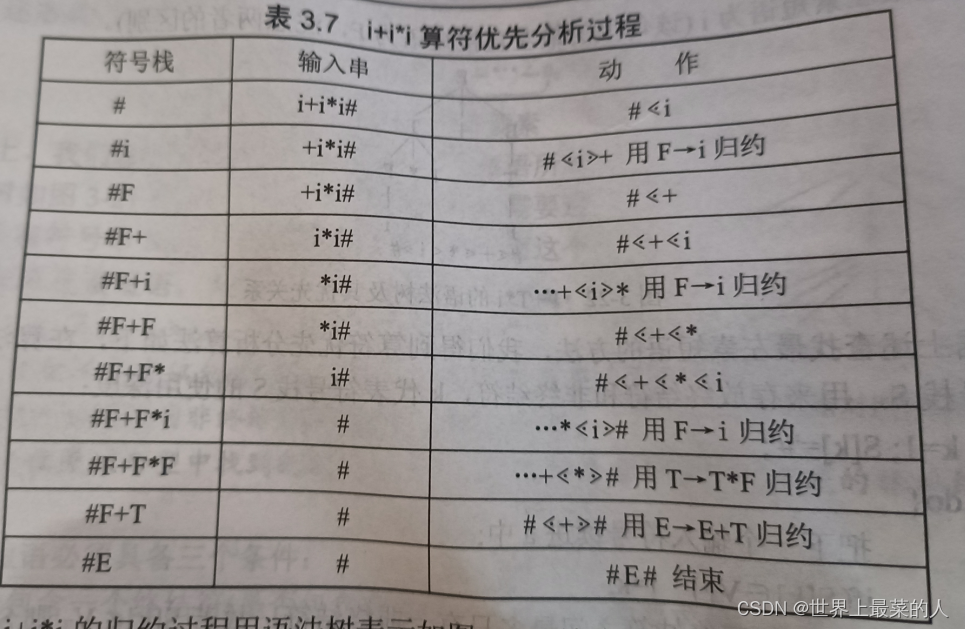
对于算符优先分析过程的求解,会给你一个式子,然后你必须根据这个式子最终转化为起始的非终结符。
根据以下的形式和终结符的关系即可得出,如下的样子: