【二叉树】Leetcode 98. 验证二叉搜索树【中等】

验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树
• 只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例1：

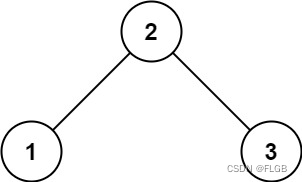
输入：root = [2,1,3]
输出：true

示例2：

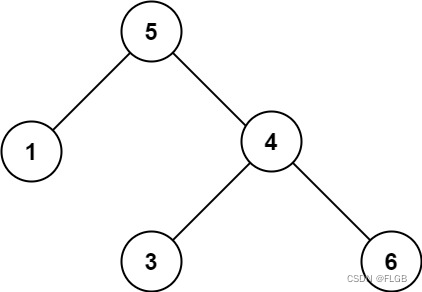
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4

解题思路1

判断一个二叉树是否是有效的二叉搜索树，可以通过中序遍历的方式来检查节点值是否按照升序排列。

• 1、进行中序遍历二叉树，递归地遍历左子树、当前节点、右子树。
• 2、在遍历过程中，记录上一个节点的值prev，初始值为负无穷。
• 3、每次访问一个节点时，比较当前节点的值与prev的值，如果当前节点的值小于等于prev的值，则二叉树不是有效的二叉搜索树。
• 4、更新prev的值为当前节点的值。
• 5、递归遍历左右子树，直到所有节点都遍历完毕

java实现1

public class IsValidBST {

    static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int val) {
            this.val = val;
        }
    }
    
    TreeNode prev = null;
    
    public boolean isValidBST(TreeNode root) {

        return isValidBSTHelper(root);
    }

    private boolean isValidBSTHelper(TreeNode root) {
        if (root == null) {
            return true;
        }

        // 判断左子树
        if (!isValidBSTHelper(root.left)) {
            return false;
        }

        // 当前节点值与前一个节点值比较
        if (prev != null && root.val <= prev.val) {
            return false;
        }
        prev = root;

        // 判断右子树
        return isValidBSTHelper(root.right);
    }

   

    // 测试示例
    public static void main(String[] args) {
        IsValidBST validator = new IsValidBST();

        // 构造一个有效的二叉搜索树
        //    4
        //   / \
        //  2   5
        // /   / \
        // 1   3  6
//        TreeNode root = new TreeNode(4);
//        root.left = new TreeNode(2);
//        root.right = new TreeNode(5);
//        root.left.left = new TreeNode(1);
//        root.right.left = new TreeNode(3);
//        root.right.right = new TreeNode(6);
//        // 判断是否是有效的二叉搜索树
//        boolean isValid = validator.isValidBST(root);
//        System.out.println("Is the tree a valid BST? " + isValid);

        //    5
        //   / \
        //  2   7
        // / \ / \
        // 1 3 6  8
        //    \
        //     4
        TreeNode root2 = new TreeNode(5);
        root2.left = new TreeNode(2);
        root2.right = new TreeNode(7);
        root2.left.left = new TreeNode(1);
        root2.left.right = new TreeNode(3);
        root2.right.right = new TreeNode(4);
        root2.right.left = new TreeNode(6);
        root2.right.right = new TreeNode(8);
        boolean isValid2 = validator.isValidBST(root2);
        System.out.println("Is the tree a valid BST? " + isValid2);
    }
}

解题思路2

使用递归的思路来判断是否是有效的二叉搜索树。

• 1、对于每个节点，都有一个取值范围（上界和下界），它的左子树节点的值应该在当前节点值的下界到当前节点值之间，而右子树节点的值应该在当前节点值到上界之间。
• 2、初始时，根节点的取值范围是负无穷到正无穷。在递归过程中，
• 不断地更新每个节点的取值范围，并判断其左右子树是否符合要求。
• 3、如果左右子树都符合，那么当前节点是有效的。在递归的过程中，
• 如果某个节点的值超出了取值范围，则说明不是有效的二叉搜索树。

Java实现2

public class IsValidBST {

    static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int val) {
            this.val = val;
        }
    }

    public boolean isValidBST(TreeNode root) {

        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    private boolean isValidBST(TreeNode node, long lower, long upper) {
        if (node == null) {
            return true;
        }
        //    7
        //   / \
        //  3   9
        // / \ / \
        // 1 5 8  10
        //  / \
        //  4  6
        if (node.val <= lower || node.val >= upper) {
            return false;
        }

        return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);
    }

    // 测试示例
    public static void main(String[] args) {
        IsValidBST validator = new IsValidBST();

        // 构造一个有效的二叉搜索树
        //    4
        //   / \
        //  2   5
        // /   / \
        // 1   3  6
//        TreeNode root = new TreeNode(4);
//        root.left = new TreeNode(2);
//        root.right = new TreeNode(5);
//        root.left.left = new TreeNode(1);
//        root.right.left = new TreeNode(3);
//        root.right.right = new TreeNode(6);
//        // 判断是否是有效的二叉搜索树
//        boolean isValid = validator.isValidBST(root);
//        System.out.println("Is the tree a valid BST? " + isValid);

        //    5
        //   / \
        //  2   7
        // / \ / \
        // 1 3 6  8
        //    \
        //     4
        TreeNode root2 = new TreeNode(5);
        root2.left = new TreeNode(2);
        root2.right = new TreeNode(7);
        root2.left.left = new TreeNode(1);
        root2.left.right = new TreeNode(3);
        root2.right.right = new TreeNode(4);
        root2.right.left = new TreeNode(6);
        root2.right.right = new TreeNode(8);
        boolean isValid2 = validator.isValidBST(root2);
        System.out.println("Is the tree a valid BST? " + isValid2);
    }
}

时间空间复杂度

• 时间复杂度：O(n)，其中n是二叉树中的节点数，每个节点都需要访问一次。
• 空间复杂度：O(height)，递归调用栈的深度为树的高度