零知识证明——zkSNARK证明体系

本笔记整理摘录自Steven Yue大佬

三个核心算法：
setup约定电路，生成随机参数
prove：证明方生成零知识证明
verify：验证方进行验证

完整性：

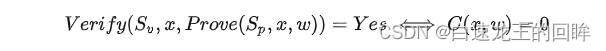
知识证明：（非常关键）
证明，证明方确实有一些我们不知道的信息，也就是这个w确确实实存在

简短证明：简短高效
零知识：公有输入x和证明pi不能暴露w

PCP定理(概率可验证定理）

所有NP难问题，都可以通过随机抽样，通过随机验证方法证明

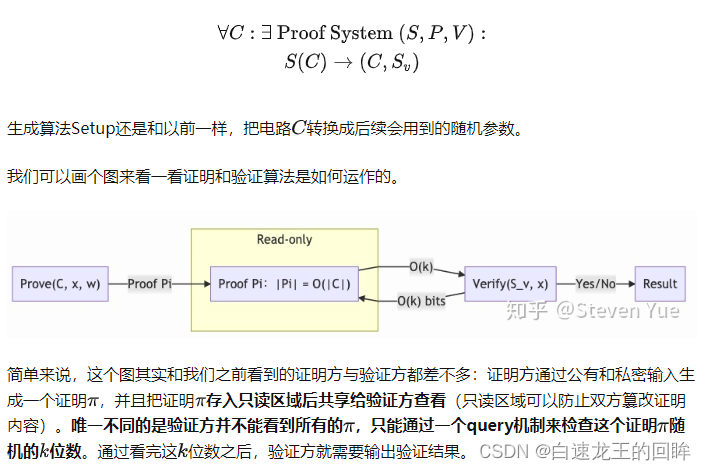
不是直接看pi了，只能在里面抽取k位

总的来说就是抽查，抽查的正确次数越多，作假的可能性越低（有点假设检验内味了）

Kilian SNARK

PCP可能有庞大的只读存储区域

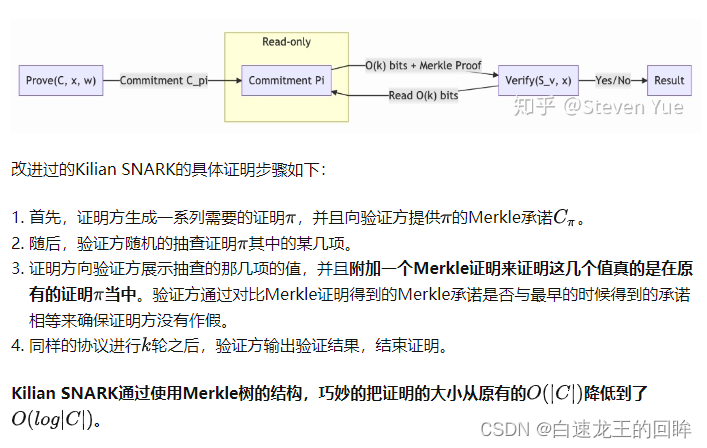
我们将readonly那里编程一个commitment
证明方展示数据的时候只需要附带一个Merkle Proof证明自己提交的数据确实是在pi中的即可
这样就可以避免存储大量的pi信息

非交互的Killian SNARK

证明方在提交证明的时候验证方无需在线，它可以在后面随机事件点来验证
需要Fiat-Shamir-Heuristic，它可以把任何交互式的随机验证协议转换为非交互式的
首先需要一个安全哈希函数H（随机预言机，无论输入的是什么，输出的值我们都可以看作是一个和输入没有关联的随机数）

改造的关键就是把验证方的随机值依赖于安全哈希函数来生成

LCPC（线性）

两个d阶的不同系数的多项式，最多只会有d个点重合
通过把证明的值当作多项式的系数，然后验证多项式在某个点的值是否相等即可

因此我们把SNARK转成多项式的形式
但是电路很难变成多项式的形式，所以需要一个叫做R1CS的程序矩阵

多项式插值，范德蒙德多项式，还原多项式的每一项系数

构造成多项式子P, Q, R
证明P® * Q® = R®

总结

PCP定理是通过随机抽查的方法来快速验证任何NP问题的解。
LPCP是约束版的PCP，讲了通过随机抽查多项式取值的方法来快速验证多项式的系数。
Fiat-Shamir Heuristic可以把一个交互式协议变成一个非交互式协议。
从一个数学运算电路出发，变换成R1CS程序矩阵之后，可以最后还原成多项式